Frequently Asked Questions

Upsampling Algorithms, Precision and Noise Shaping

Reconstruction accuracy in the context of upsampling refers to how well the upsampled signal approximates the original (analog) signal. It is a measure of how closely the interpolation process used during upsampling preserves the characteristics and fidelity of the original audio signal. This is crucial for maintaining audio quality and avoiding artifacts.

Reconstruction accuracy depends on the quality of upsampling algorithm and/or filters used, the precision of the calculations, and the application of noise shaping. The choice of upsampling algorithm is critical as it determines how the new samples are generated. The precision of the calculations affects the accuracy of the interpolation process, with higher precision leading to more accurate reconstruction. Noise shaping is used to reduce quantization noise, which can introduce artifacts in the upsampled signal. By shaping the noise, quantization noise it is moved to frequencies where it is less audible, preserving the accuracy of the signal and improving the overall audio quality.

Note: Even though typical recorded music is limited in precision to a maximum of 32bits, it is still beneficial to use higher precision for the upsampling process. This is because:

• The upsampling process involves multiple calculations and the use of higher precision helps to reduce the accumulation of errors and maintain the accuracy of the reconstructed signal.
• During the upsampling process, the intermediate samples that are added can have a much higher precision than the original samples and are critical to the perceived quality of the reconstructed signal.

Evaluating Reconstruction Accuracy

In order to evaluate the reconstruction accuracy of an upsampling algorithm, we need to compare the upsampled signal with the original signal sampled at the same rate as the upsampled signal. It is easier to do this comparison with simulated signals as we do not have access to recorded music signals at different rates in a controlled setting. For the purpose of demonstration, we can use band-limited signals that are generated at a lower rate (1fS: 44.1kHz) and upsampled to a higher rate. The upsampled signal can then be compared with the same band-limited signal generated at a higher rate (16dfS: 705.6kHz) to evaluate the accuracy of the upsampling algorithm.

For the purpose of this demonstration, we chose a Band-Limited 44Hz Saw-Tooth (BLST) signal generated at 44.1kHz and upsampled it to 705.6kHz using various algorithms including PGGB. We chose BLST as it is harmonic rich with harmonics stopping just short of the Nyquist frequency (22.05kHz), it also has very steep rising edge and a slow decay. Below is the time domain and frequency response of BLST signal we used.

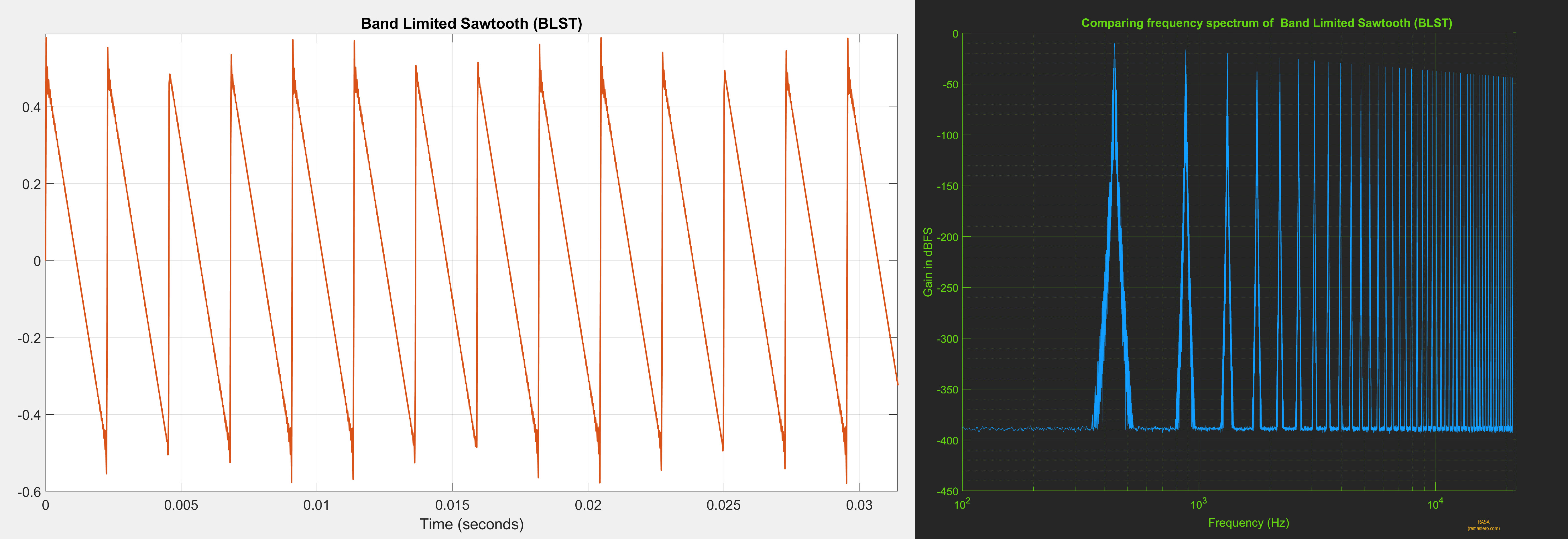
Note: BLST is a stationary, periodic signal and unlike much more complex music signals. It is a good test signal to objectively establish the base line for reconstruction accuracy. If an upsampling algorithm cannot accurately reconstruct BLST, it is even less likely to accurately reconstruct more complex signals.

Comparing Algorithms

Using the 44.1kHz sawtooth signal as input we can now compare the reconstruction accuracy of upsampling algorithms at different precisions. We will look at time domain plots, frequency spectrum of the upsampled signals and also spectrum of the error (i.e., the difference between the reference signal and upsampled signal).

For perfect reconstruction, the upsampled signal should be identical to the reference signal both in time and frequency domain. The error spectrum should be flat and close to the quantization noise floor.

1. PGGB

   PGGB is non-apodizing, with a near ideal transition band and very high attenuation. It uses all the information in the signal and is designed to provide near ideal reconstruction of the original signal. Below are the results of upsampling the BLST signal to 705.6kHz using PGGB at 107 bit precision. The time domain and frequency spectrum of the upsampled signal are shown below.

   

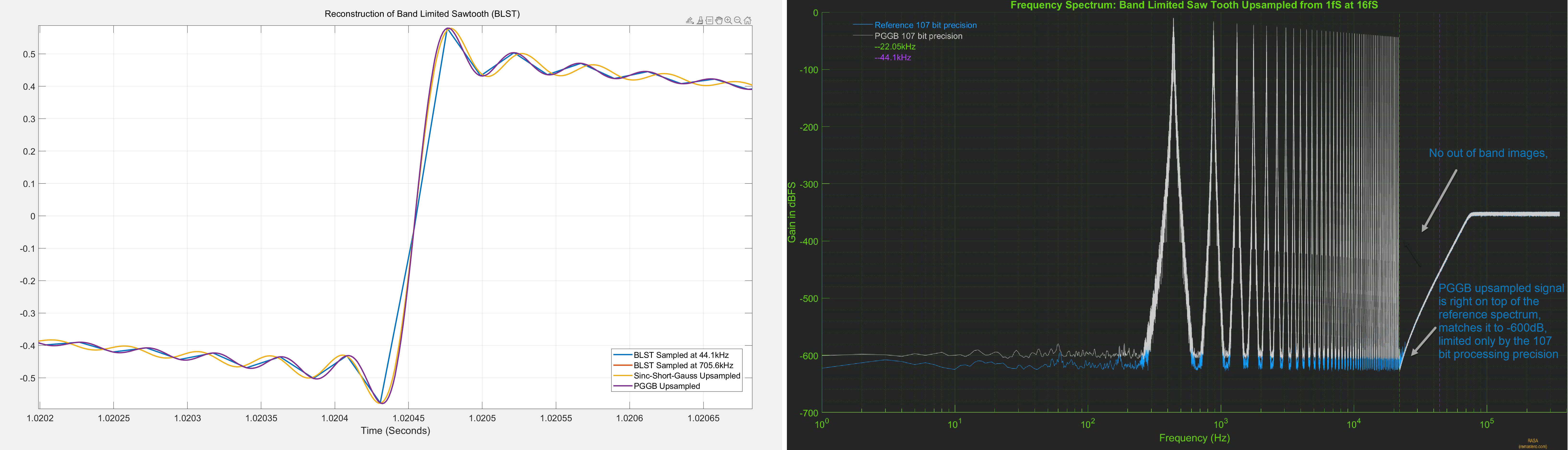   The reference signal was directly generated at 107 bit precision at 705.6kHz. The plot on the left is the time domain plot, zoomed into one of the rising edges of the sawtooth signal. The PGGB upsampled signal (purple) is right on top of the reference signal (red) and is indistinguishable. The plot on the right is the frequency spectrum of the PGGB upsampled signal (grey) and the reference signal (blue). Here too, PGGB is right on top of the reference signal and matches it up to -600dB!. We see the same behavior for all precisions (64 bits to 256 bits), irrespective of the precision used, the PGGB upsampled signal matches the reference signal, limited only by the noise floor of the precision used.

   Because the PGGB upsampled signal is right on top of the reference signal both in time and frequency domain, it is hard to tell if there is any difference. It is easier to illustrate reconstruction accuracy by plotting the spectrum of error between the reference signal and PGGB upsampled signal. Below is the plot of the spectrum of the error at all precisions. It clearly shows there are no errors in-band (which includes the audible range). There are no out of band errors either, because all the high frequency images are fully attenuated. What is seen is close to a flat line corresponding to the quantization noise floor for the precision used.

   

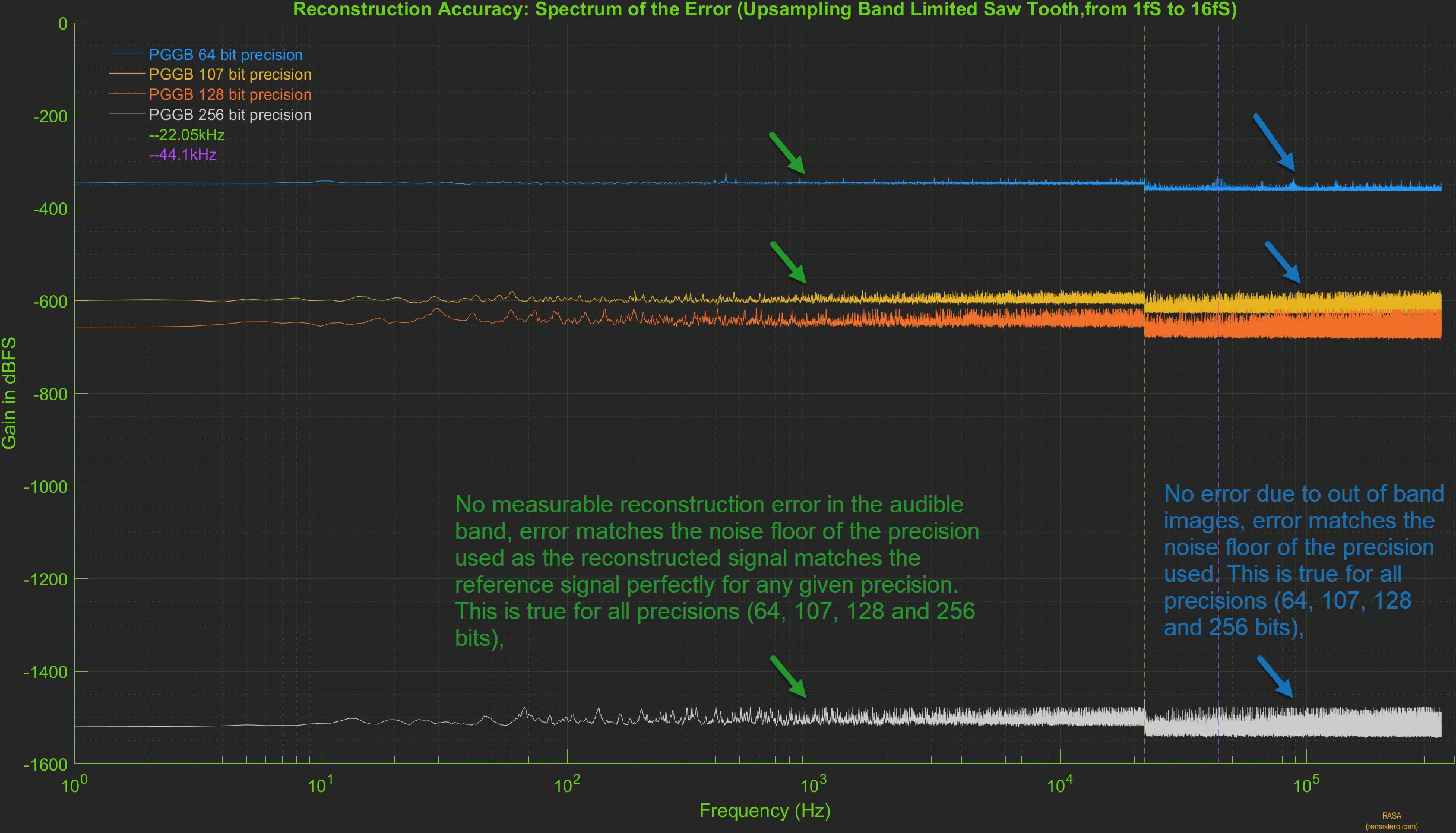
   Form the above plots, we clearly see that in the case of PGGB, the reconstruction accuracy is limited only by the quantization noise floor. This is where Noise Shaping plays a big role. If a simple 24 bit or 32 bit dither were to be used, then the reconstruction accuracy will be limited to -200dB or higher and using higher precision would be counter productive.

2. Short Apodizing Filter (4k Gaussian Windowed Sinc)

   Short apodizing filters are designed to have a short impulse response and roll-off close to or slightly earlier than 20kHz with the intent to remove any aliasing artifacts already present in the signal. For this analysis, we chose a linear phase sinc filter with 4065 taps and a corner frequency of 20.5kHz, and used an Approximate Confined Gaussian window (ACGW) with alpha = 0.065. Below are the results of upsampling the BLST signal to 705.6kHz using the short apodizing filter using 107 bit precision. The time domain response of the upsampled signal are shown below.

   

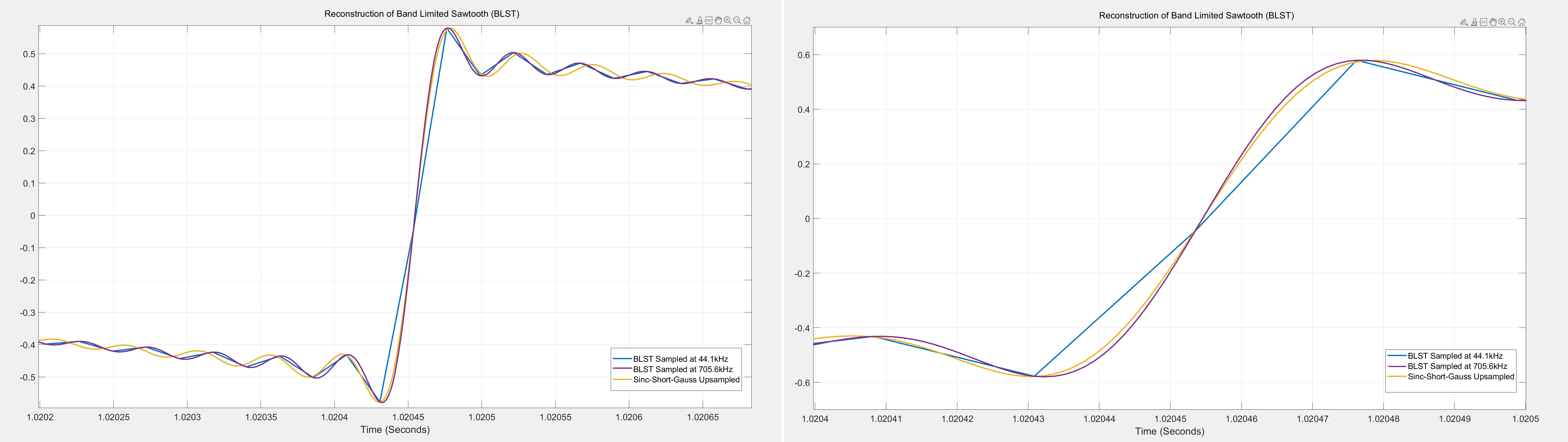   The reference signal was directly generated at 107 bit precision at 705.6kHz. The plot on the left is the time domain plot, zoomed into one of the rising edges of the sawtooth signal. The short apodizing filter upsampled signal (yellow) does not match reference signal (purple) and is clearly distinguishable. The plot on the right is further zoomed to show the rising edge and it is very clear that the upsampled signal (yellow) is slower (with a slightly less steep slope) compared to the reference signal (purple). This behavior should not be surprising given the apodizing nature of the filter attenuates the higher order harmonics present in the signal. This attenuation will be further evident in the frequency spectrum of the upsampled signal

   

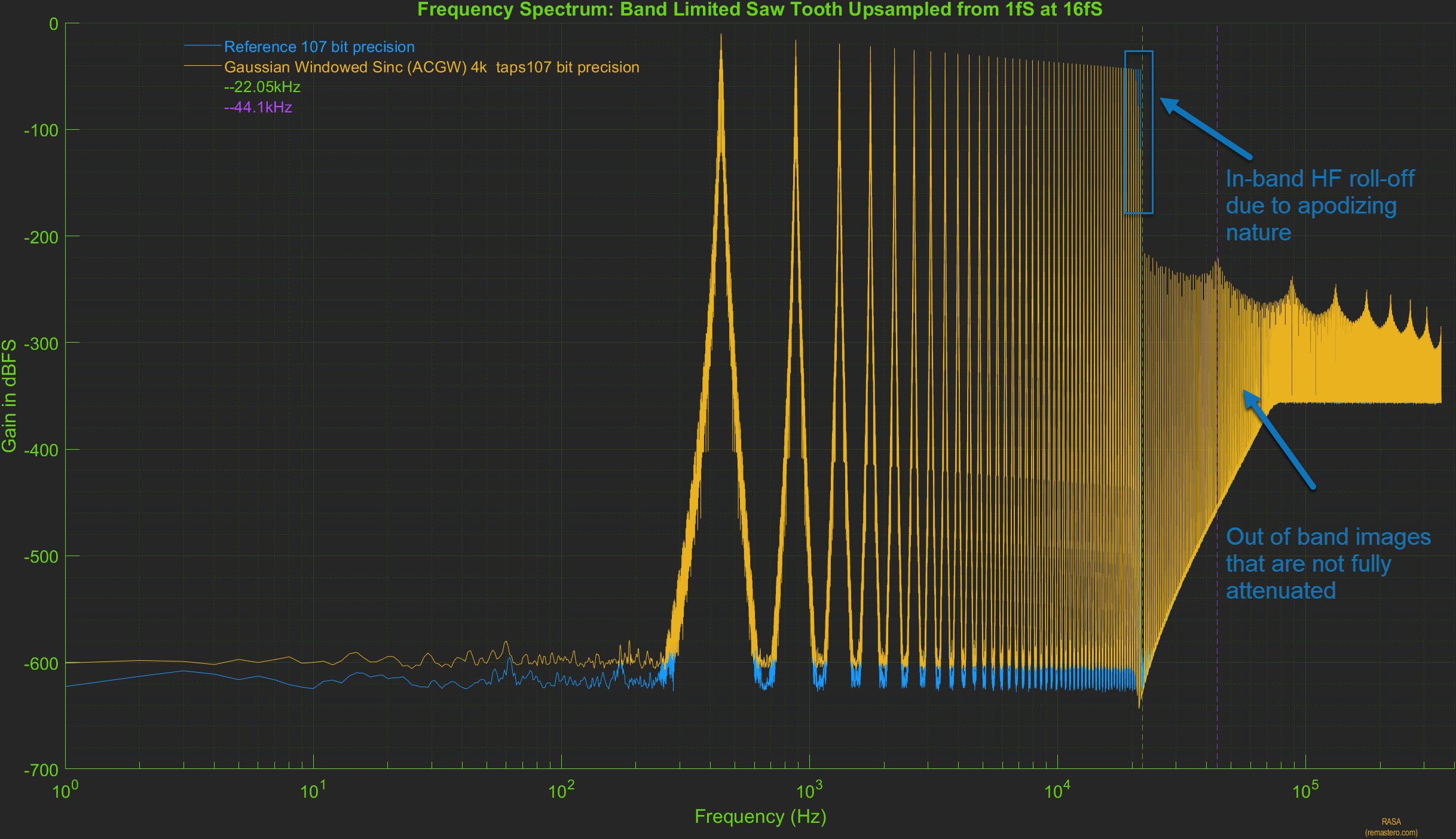   In the plot above, the frequency spectrum of the upsampled signal using the short apodizing filter (yellow) is shown. Compared to the spectrum of the reference signal (blue), the in-band high frequency roll off can be seen starting close to 20khz, thus attenuating the higher harmonics present in the original signal. The out of band high frequency images are not fully attenuated either and this too is evident after the Nyquist frequency of 22.05kHz. However, in the audible range, it is very hard to tell them apart as the spectrum of the upsampled signal is right on top of the reference signal.

   Here too, it is easier to evaluate the reconstruction accuracy by plotting the spectrum of error between the reference signal and short apodizing filter upsampled signal. Below is the plot of the spectrum of the error at all precisions (on the left). It clearly shows there are three types of error present. Error in the audible range, error due to high frequency roll-off due to apodizing nature of the filter and error in the out of band range as the HF images are not fully attenuated. These errors are due to a combination of factors such as the length of the filter, the window used and the corner frequency of the apodizing filter.

   

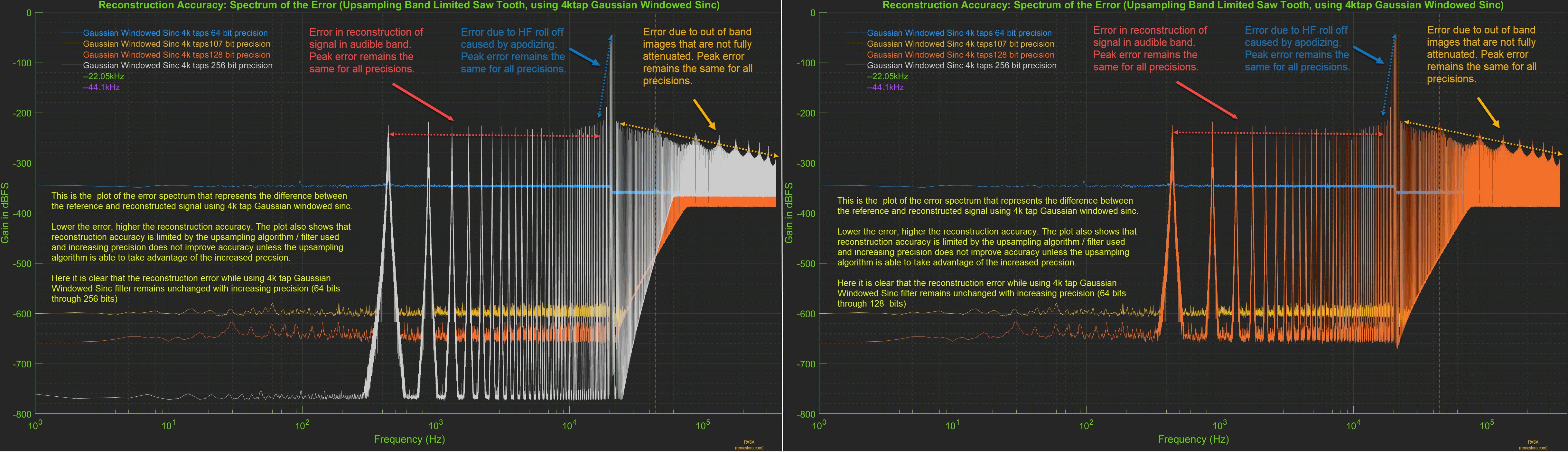
   From the above plots, we clearly see that in the case of short apodizing filter, the reconstruction accuracy is limited by the filter design. The reconstruction error remains unchanged with precision, increasing precision reduces the quantization noise floor but the peak error remains unchanged. In the plot on the right, we have removed the error spectrum for 256 bit precision to reveal the error at 128 bit precision. When the upsampling algorithm used is not accurate, it is counter productive to increase the precision and 64 bit precision would suffice for this filter.

   Objectively, it is easy to see that this is a far-cry from the near ideal reconstruction seen with PGGB. next, let us see if some of these issues can be remedied by using a long sinc based filter that is non-apodizing

3. Long Non-Apodizing Filter (2M Flat-top Windowed Sinc)

   For this next analysis, we chose a long linear phase sinc filter with 2 million taps, it is non apodizing with a corner frequency that matches the Nyquist frequency of 22.05khz, and used the HFT248D Flat Top window that provides 248db of side lobe attenuation. We chose this filter to illustrate 1. if increasing the number of sinc coefficients can improve the reconstruction accuracy, 2. if the combination of longer filter and the flat top window provides better suppression of out of band HF images and 3. to avoid any intentional attenuation of in band high frequency signals. Below are the results of upsampling the BLST signal to 705.6kHz using the long non-apodizing filter using 107 bit precision. The time domain and frequency spectrum of the upsampled signal are shown below.

   

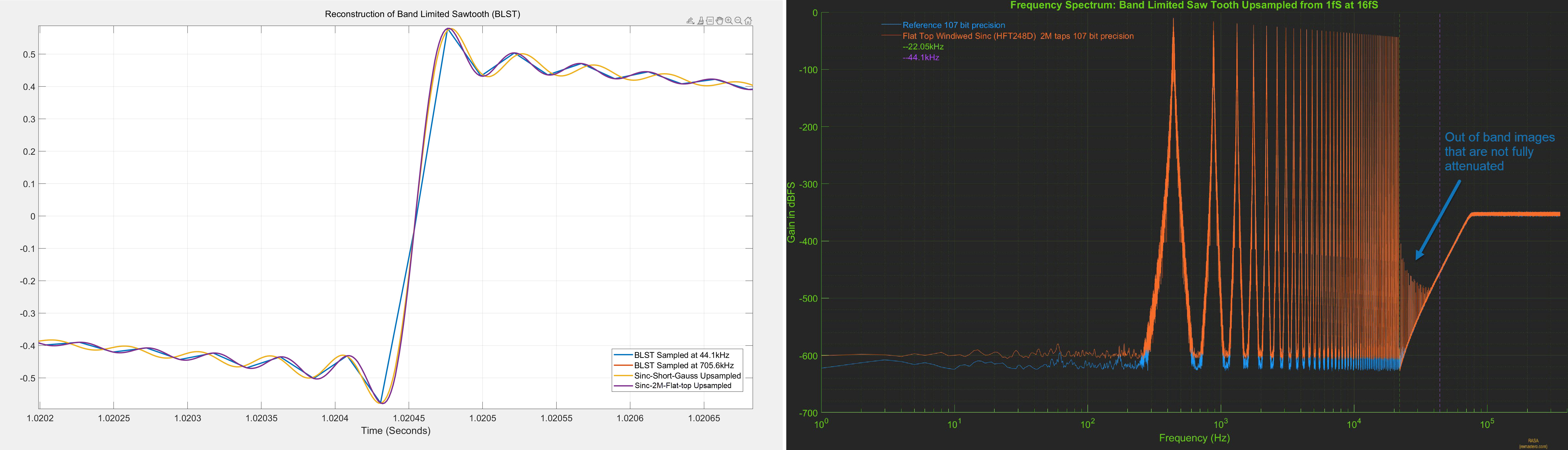   As before, the reference signal was directly generated at 107 bit precision at 705.6kHz. The plot on the left is the time domain plot, zoomed into one of the rising edges of the sawtooth signal. The 2M Sinc upsampled signal (purple) is right on top of the reference signal (red) and is indistinguishable. The plot on the right is the frequency spectrum of the 2M sinc upsampled signal (orange) and the reference signal (blue). Here the spectrum of 2M sinc upsampled signal is right on top of the reference signal until the Nyquist frequency of 22.05khz, but unlike PGGB upsampling, we still see out of band images that are not fully attenuated.

   We further evaluate the reconstruction accuracy of the 2M sinc filter by plotting the spectrum of error between the reference signal and 2M sinc filter upsampled signal. Below is the plot of the spectrum of the error at all precisions. It clearly shows there are two types of error present. Error in the audible range, error in the out of band range as the HF images are not fully attenuated. While the longer filter and the flat-top window helped in decreasing both in-band and out of of band errors, it is not near perfect as we saw with PGGB upsampling.

   

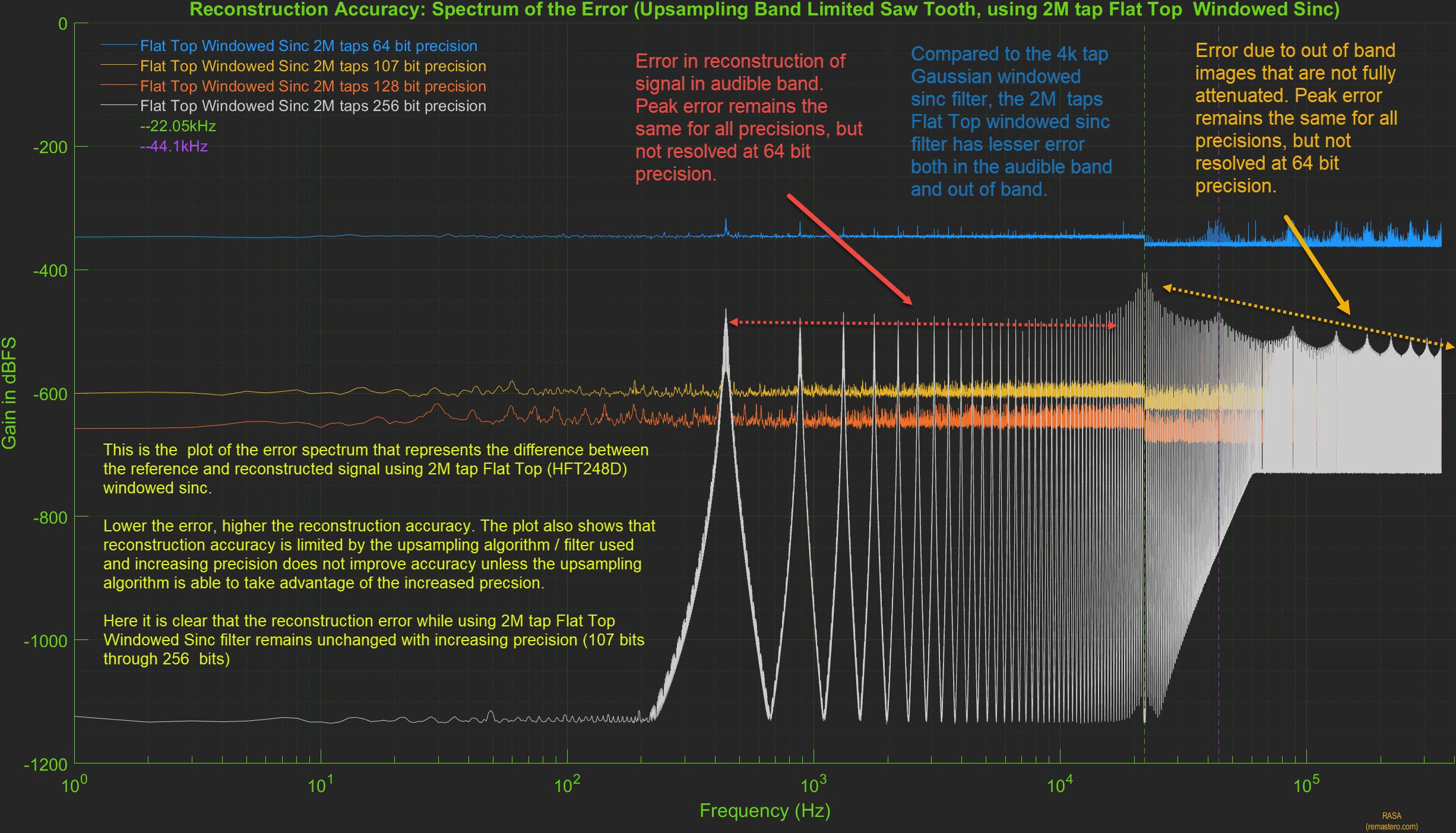
   From the above plot, we clearly see that the reconstruction error remains unchanged with precision, increasing precision reduces the quantization noise floor but the peak error remains unchanged. In the case of the 2M sinc filter, it will be counter prodctive to use precisions higher than 75 - 80 bits.

4. Medium Non-Apodizing Optimized Filter (250k Optimized Windowed Sinc)

   We showed previously that even though the long sinc filter with 2M taps did not provide near ideal reconstruction accuracy, it improved significantly over the shorter Gaussian filter. Though the longer sinc filter provided better reconstruction accuracy and better attenuation of out of band images, the filter was not designed with reconstruction accuracy in mind. One can do a lot better with even a shorter filter if the filter can retain more of the original sinc coefficients and at the same time, the window tapper is optimized to achieve better attenuation of out of band images. In fact, this was the approach in the windowed sinc functions used by earlier versions of PGGb (V3 and older). For this analysis, we chose a linear phase, medium length (250k tap) sinc filter, it is non apodizing with a corner frequency that matches the Nyquist frequency of 22.05khz, and we use our proprietary optimized window. We chose this filter to illustrate that a medium length filter can easily improve over a much longer filter if properly designed. Below are the results of upsampling the BLST signal to 705.6kHz using the medium non-apodizing filter using 107 bit precision. The time domain and frequency spectrum of the upsampled signal are shown below.

   

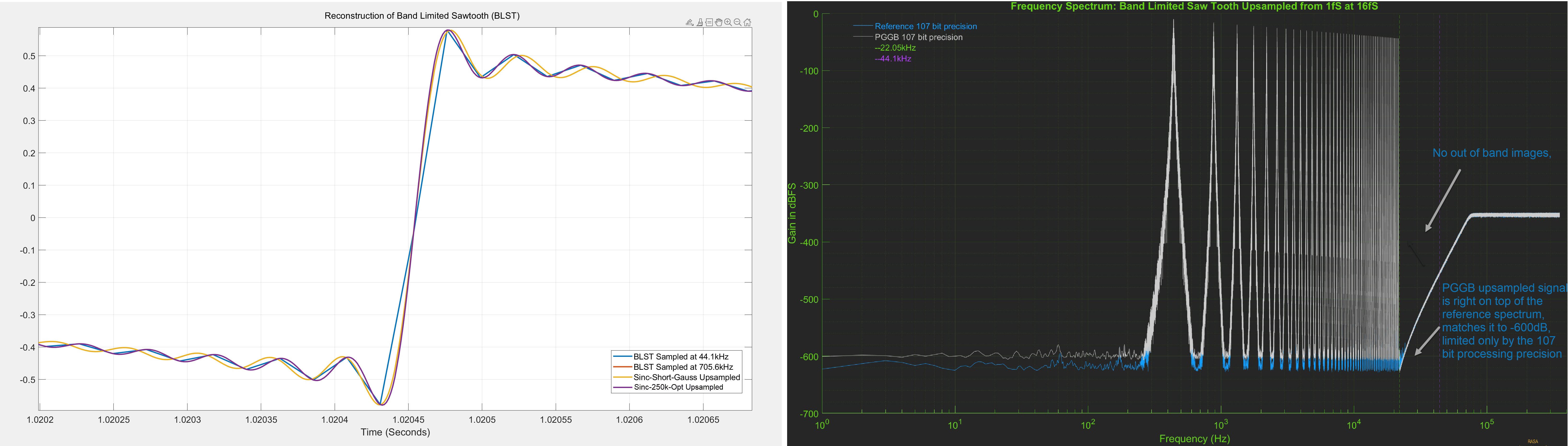   As before, the reference signal was directly generated at 107 bit precision at 705.6kHz. The plot on the left is the time domain plot, zoomed into one of the rising edges of the sawtooth signal. The 250k Sinc upsampled signal (purple) is right on top of the reference signal (red) and is indistinguishable. The plot on the right is the frequency spectrum of the 250k optimized sinc upsampled signal (grey) and the reference signal (blue). Here the spectrum of 250k sinc upsampled signal is right on top of the reference signal until the Nyquist frequency of 22.05khz, but unlike the longer 2M sinc filter, we do not see any out of band images, they are not fully attenuated up to the noise floor of 107 bit precision.

   We further evaluate the reconstruction accuracy of the 250k optimized sinc filter by plotting the spectrum of error between the reference signal and 250k optimized sinc filter upsampled signal. Below is the plot of the spectrum of the error at all precisions. We do not see any errors at 64 bit, 107 bit and 128 bit precision, but we see some error near the Nyquist frequency at 256 bit precision we also see that at 256bit, the noise floor is higher than what we saw for PGGB upsampling.

   

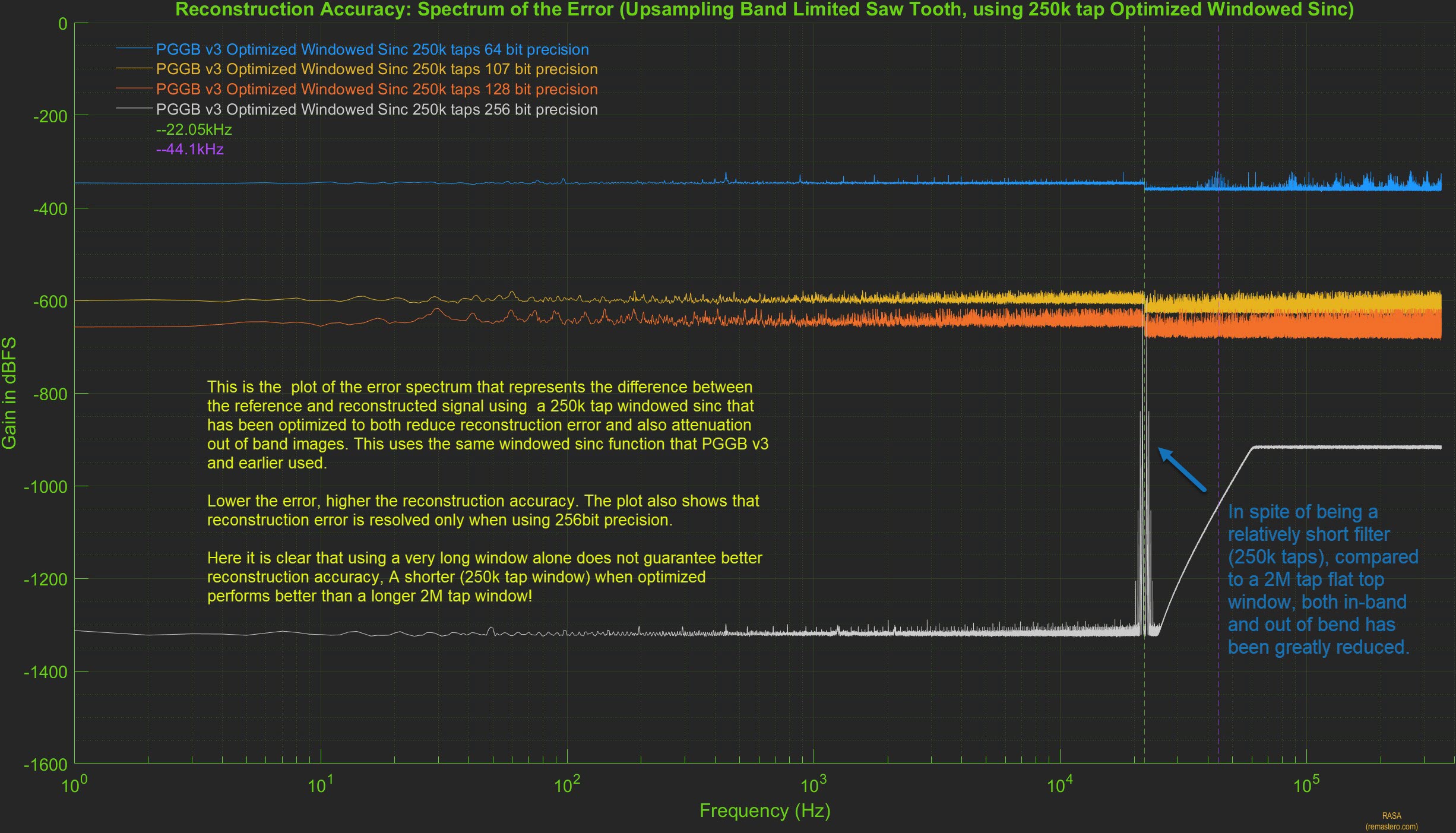   This shows that when properly designed with reconstruction accuracy in mind, a medium length filter can provide much better reconstruction accuracy, but it may still fall short of the near ideal reconstruction accuracy provided by PGGB which does not use a windowed sinc function.

The Takeaway

We showed that reconstruction accuracy is affected by the type of upsampling algorithm used and that in-band reconstruction error exists even for a relatively simple periodic signal such as the sawtooth waveform. Increasing precision only helps if the upsampling algorithm is accurate and if noise shaping can be used. The PGGB upsampling algorithm provides near ideal reconstruction accuracy, limited only by the quantization noise floor for the precision used.

Don't test outside of spec!

Many of these myths arise because of either lack of full understanding of sampling theory or misinterpreting it. First, it is important to understand a reconstruction or upsampling algorithm cannot be analyzed by just passing an impulse (pop transient) or a step response. Impulse and step signals have their use, i.e., to understand the frequency and time domain response of a system, but they are not the best way to test a reconstruction/upsampling algorithm. In fact, they are the worst signals you could use to do such a test. It is like testing an equipment outside it's operating range and expecting good results! Sampling theory only guarantees perfect reconstruction when the signal is perfectly band-limited. We understand this is the ideal case and no signal is perfect, so what would be a better test signal? Choose your pick:

• Pure impulse or step: Impulse or step signals are not band limited and have infinite bandwidth and are the polar opposite of what is guaranteed to work.
• impulse or step that is band-limited: Impulse or step that are band-limited, need not be perfect, they should have passed through a low pass filter similar to what ADC would do. Granted, they will still have some aliasing and ringing, but at least it is a test signal that is closer to what a music signal is and also does not totally disregard the conditions for prefect reconstruction. Even if the low pass filter is not a great one, it is still infinitely better test signal.

One example of incorrect testing of resampling algorithms is creating Dirac pulses (pop transients) at high rate (say 352.8k), convert those to 44.1k using the algorithm under test, and finally convert those back to the original rate (352.8k). Dirac pulses do not exist in recorded music signals. Mic pop or clip may be, but they have to pass through the ADC first, which will band limit such pops or transients. Digital reconstruction is about reconstructing the original signal from sampled analog signals that are band-limited, a dirac pulse has no place in such a test as it is of a purely digital origin. The right test would have been to use a filter similar to the ones typically used in an ADC to convert the Dirac pulses from the high rate to 44.1kHz. Then use that signal as an input for testing the reconstruction algorithms.

Bottom line: If an upsampling algorithm is developed based on using non-band-limited signals to test its accuracy (which violates the very basic requirement for reconstruction), it would be calibrated quite differently. It is the equivalent of using English units on a system designed with metric units in mind.

Three wrong reasons

Here are some common misconceptions associated with resampling the PGGB way (i.e., Non-apodizing, using all the information, narrow transition band with high attenuation).

1. Wrong reason 1: Rings like a bell (maybe for a bat)

   It is often claimed that the steep and narrow low pass behavior of PGGB in the frequency domain will result in audible ringing in the time domain. This is simply not true, there will be no ringing if the signal is band-limited (i.e. if it only contains frequencies that are less than half the sample rate). No signal is perfect, if the music was recorded and already went through an ADC, then it is already band-limited as it cannot contain any frequencies above half the sample rate. For CDs, the only content in music that can trigger ringing is one exactly at 22.05kHz where there is very little present because the ADC already attenuated it. The exception is clipped music during post processing, but here too, any ringing one can observe will be exactly at 22.05kHz for CD rates, way beyond normal human hearing (more on audibility).

   The whole idea of ringing is way exaggerated (because PGGB's corner frequency is exactly at half the sampling rate). Any ringing one may see will be at 22.05kHz because of the residual energy at the corner frequency left by the ADC, this will not be any more (in peak level) than what you may find with relatively short filters. Any ringing that is already present because of the ADCs filter is left untouched by PGGB and this too is beyond the audible range.

   It is easy to demonstrate this with a simple example. We created a 44.1kHz impulse train with multiple, closely spaced Dirac ('pop') transients like the one below.

   

   Then to make this an acceptable test signal, we passed it through an IIR filter with a corner frequency at 21kHz to make it band-limited and create a 44.1kHz test file. This is not a perfect band-limited signal, but it is a much better test signal. You can see the band-limited impulse signal below. You will see it is not perfect, but it still retains the two transients, and as expected it shows the time domain response of the ADC filter. It is not an infinite band-width signal anymore.

   

   We then used PGGB to upsample it 16x using default settings and 128bit precision and created a 705.6kHz upsampled file. We then used a short linear phase Gaussian apodising filter to upsample to the same 705.6kHz. The Gaussian filter we used is a short Gaussian polyphase sinc filter, the Gaussian filter's time domain response is provided below.

   

   Below we show the results (you can click on the image to make it bigger). Blue (PGGB), Red (Short Gauss) and Yellow is the original. We only zoomed in on one set of transients, but the same is true with all of the transients. You will notice that:

   • You can make out the two transients clearly in all three signals
   • There is some pre-ringing in the PGGB upsampled signal, this is expected because the band-limiting filter is not perfect, but you can see very little. Which again is beyond the audible range to cause any change in perception of the transient.
   • Ironically, there is pre-ringing even in the short Gauss upsampled signal and this is more than what you see with PGGB. To be fair, you will not hear this either.
   

   We zoom in on the pre-ringing portion of the first transient to show the time domain response of the three signals. Here you can clearly see the pre-ringing in the short gauss signal is more than the PGGB signal

   

   Now let us repeat the above test with a real track. For this test we chose a 44.1kHz track that has a lot of clean transients and also contains clipping. The track is '08 Bright Mississippi' from the album The Roy Haynes Trio Featuring Danilo Perez And John Patitucci and was downloaded from Qobuz. We upsampled this track to 705.6kHz using PGGB and short Gaussian polyphase sinc filter, the same as the one we used above. We set the gain to -1.5dB to prevent limiting or clipping and then scaled it back by +1.5dB so we can compare the signals. We also used Gaussian dither for both PGGB and the short Gauss filter to make the comparison fair. The time displayed on the x axis is in seconds and will match the time in the original track. We zoom in on a section where there was a rim hit and the track clipped. Below we show the results (you can click on the image to make it bigger). Blue (Original), Red (Short Gauss) and Yellow is the PGGB. You can see that:

   • PGGB does a near perfect job of reconstruction, passing through each of the original samples even when they clipped.
   • The short Gaussian filter both undershoots and overshoots compared to PGGB, this very similar to what we demonstrated previously regarding pre-ringing.
   • It is very easy to see that PGGB does better even when the signal clipped, because the signal has been band-limited already.
   

   The only time significant ringing can be shown is when it is either an artificial signal (such as an impulse, step) with no band-limiting or if post processing causes clipping. Even if clipping is present this ringing is at half the sample rate which for CD is 22.05kHz, which is beyond the human hearing range, it does not affect signals in the audible range, and is barely noticeable!

   So, if someone listens to a whole lot of artificial signals instead of music, or a lot of clipped music, and they have an extended hearing range beyond 20kHz, we can understand their concern. But for the rest of us, it is a non-issue.

---

2. Wrong reason 2: Blurs transients (show us your math)

   It is claimed that long linear filters will cause transient blurring because they are using information both from the future and the past to reconstruct transients and hence both future and past samples could potentially affect a transient that is being reconstructed presently. First, PGGB does not use such filters, so this argument is moot. But even if it did, the argument is pure conjecture without a mathematical basis. If this were true then the whole sampling theorem would fall apart because it is built on the premise of being able to use infinitely long sinc based linear filters to perfectly reconstruct band-limited sampled signals. Anyone claiming so should support their argument with a mathematical proof.

   It is fairly simple to demonstrate this with real music tracks, but we chose the more dramatic example of band-limited impulses we used previously. We then used PGGB to upsample band-limited, closely spaced Dirac pulses (pop transients) at 44.1kHz to 705.6kHz using default settings and 128bit precision. We also used a short minimum phase filter which is recommended by some as an ideal filter for music containing strong transients such as pop and rock. minimum phase version of short polyphase sinc filter, the filter's time domain response is provided below.

   

   Below we show the results (you can click on the image to make it bigger). Blue (PGGB), Red (short mp) and Yellow is the original. We only zoomed in on one set of transients, but the same is true with all of the transients. You will notice that:

   • You can make out the two transients clearly in the original signal and the one upsampled by PGGB
   • The short mp filter which is recommended for music with transients ironically is the one that blurs the transients!
   • The only saving grace for short mp filter is that there is no pre-ringing (which is beyond the audible range anyway, but it comes at the huge cost of post ringing and blurred transients!
   

   Now let us repeat the above test with a real track. For this test we chose a 44.1kHz track that has a lot of clean transients, the same one as before. The track is '08 Bright Mississippi' from the album The Roy Haynes Trio Featuring Danilo Perez And John Patitucci and was downloaded from Qobuz. We upsampled this track to 705.6kHz using PGGB and minimum phase version of short polyphase sinc filter, the same as the one we used above. We also used Gaussian dither for both PGGB and the short Gauss filter to make the comparison fair. The time displayed on the x axis is in seconds and will match the time in the original track. We zoom in on a section where there was a clean transient when two drum sticks were hit together. The results are shown below (you can click on the image to make it bigger). Blue (Original), Red (Short mp) and Yellow is the PGGB. You can see that:

   • PGGB does a perfect job of reconstruction of the transient, passing through each of the original samples.
   • The short mp filter misses the start of that transient, overshoots and distorts.
   • It is very easy to see that PGGB does a perfect job of reconstructing transients, there is no blurring.
   

---

3. Wrong reason 3: Oversampling filters affect outcome only above audible band (why so naive?)

   It is sometimes argued that ringing that is outside of human audible range, can have audible effects on the in-band music. The reasoning given is that, if this were not true, all oversampling filters and all DAC's internal upsampling should sound the same, because they only affect the out-of-band signal. This is a rather naive argument that focuses only on the frequency domain! it assumes these filters do not affect the time domain transients, transient reconstruction and reconstruction of small signals. All these filters sound different not because we are super human and suddenly hear above 20kHz. While evaluating DACs or digital oversampling filters, it is important to focus on time domain cues such as depth, layering, resolution and transient quality, not tonality. Because every change we make to the reconstruction algorithms affect how the transients are reconstructed in the time domain and in turn, affects our perception of transients and the construction of the virtual soundscape.

   This too is very easy to illustrate with the very same example that we used previously. We compare the original band-limited signal (yellow) with the PGGB upsampled signal (Blue) and the short mp upsampled signal (Red).

   • You can clearly see how the transients are reconstructed differently by PGGB and short mp filter
   • The short mp filter which is recommended for music with transients blurs the transients, while PGGB preserves them just fine.
   • PGGB will sound different from short mp filter not because of any pre-ringing that is beyond the audible range, but because it is more faithful to the original transients. However short mp that blurs transients will sound flat lacking depth (which may be fine for some music like Rock). The blurring of transients that can lump the energy in to 'clumps' could give the perception of stronger transients, and it is a smoother and more forgiving sound. For that reason it could still be good for music such as rock and pop.
   

   Now let us repeat the above test with a real track using the same one as before. The track is '08 Bright Mississippi' from the album The Roy Haynes Trio Featuring Danilo Perez And John Patitucci downloaded from Qobuz. We upsampled this track to 705.6kHz using PGGB and minimum phase version of short polyphase sinc filter, the same as the one we used above. We also used Gaussian dither for both PGGB and the short minimum phase filter to make the comparison fair. The time displayed on the x axis is in seconds and will match the time in the original track. We zoom in on a section where there was a clean transient when two drum sticks were hit together. The results are shown below (you can click on the image to make it bigger). Blue (Original), Red (Short mp) and Yellow is the PGGB. You can see that:

   • PGGB does a perfect job of reconstruction of the transient, passing through each of the original samples.
   • The short minimum phase filter misses the mark many times, overshoots and also distorts.
   • PGGB clearly demonstrates better reconstruction accuracy here. The obvious change in shape of the reconstructed waveforms will have an audible effect.
   

   As another example, we use the same track again, but we chose a relatively quiet part of the track and we upsampled this track to 705.6kHz using PGGB and short Gaussian polyphase sinc filter. We also used Gaussian dither for both PGGB and the short Gauss filter to make the comparison fair. The time displayed on the x axis is in seconds and will match the time in the original track. Below we show the results (you can click on the image to make it bigger). Blue (Original), Red (Short Gauss) and Yellow is the PGGB. You can see that:

   • The Magic of Whittaker-Shannon interpolation formula guarantees near perfect interpolation, passing through each of the original samples even for this relatively low level signal.
   • The short Gauss filter reconstructs differently in comparison which is easily observable in time domain, but the differences are small.
   • It is very easy to see that PGGB reconstructs low level signals differently, and why they could be audibly different be it transients or low level detail.
   

---

Let us show you how oversampling filters affect outcome in the audible band too!

One way to illustrate how oversampling filters can affect the outcome in the audible band is by plotting the difference between the same audio track that was upsampled with two different oversampling filters in both time domain and in the frequency spectrum. But there are a few challenges in accomplishing this:

1. The first challenge is it is very hard to align the two upsampled signals perfectly at a sample level to do the comparison. Depending on the upsampling algorithm used, they could introduce a sub-sample shift that would make the differences look much larger than they truly are. The solution is not to try and align the signals by correcting for the sub-sample shift. This is because, any processing can alter the signals we are trying to compare and invalidate the comparison. Since PGGB does not introduce a sub-sample shift, the only way to do this comparison is to choose a filter that does not introduce a sub-sample shift, so we chose the sinc based halfband filter.
2. The second challenge is that though we can relatively easily plot the differences in time domain, it is harder to show the differences in the frequency spectrum using FFTs. This is because, subtle yet audible differences in the audible range get averaged out.

The best way to illustrate this is instead look at the reconstruction error spectrum of the difference between the two upsampled signals. This is done by taking the difference between the two upsampled signals and then plotting the frequency spectrum of that difference. This is discussed in detail in the reconstruction accuracy section.

Did we pretend Gibbs phenomenon did not exist and defy physics?

Please do not jump to any such conclusions. If you are wondering Gaussian filters have the most compact time-frequency footprint, then how is it plausible that PGGB has less peak ringing than a short Gaussian filter? As far as the plots go, what you see is what you get, so it is mathematically possible. The answer lies in the corner frequency. The Gaussian filter we used is a short Gaussian polyphase sinc filter (it is not a minimum phase filter), the Gaussian filter's time domain response is provided below.

The Gaussian filter is linear, and apodizing and has a corner frequency earlier than the Nyquist, while PGGB has a corner exactly at 22.05kHz. Any ringing you see in time domain is the result of the filter having to dissipate the energy beyond its cutoff frequency. So as the filter's cutoff frequency increases, the ringing will become more localized in time (i.e., will also increase in frequency) because it only needs to dissipate the energy that exceeds the cutoff frequency, everything else just passes through. So PGGB will ring exactly at 22.05kHz for CD rates and every other frequency just passes through.

An apodising filter has to deal with all the leftover energy starting from its cutoff frequency till the Nyquist that was left unfiltered by the ADC which will be more than what PGGB has to filter. While PGGB has to deal with whatever little energy that is left at the Nyquist after the ADC has already done what it can. So, it is not entirely surprising that you see less ringing with PGGB on a reasonably band-limited signal. Here by 'less' we mean the peak magnitude of pre-ringing (after all, the peak magnitude prior to a transient is likely to affect transient perception, if it is even audible!). Ultimately this is all about law of conservation of energy. A short filter has to dissipate the residual energy past its corner frequency within its time domain footprint, the shorter it is, the more it has to dissipate within the short duration. So this is a function of both the length of the filter and its corner frequency. The peak pre-ringing for PGGB can be less, though the duration can be longer, with a lower magnitude. So we did not cheat Gibbs, and again this is all beyond the audible range.

Of course, the less performant the ADC filter is and you push the corner frequency of the ADC filter further out you will see more ringing with PGGB till the ADC's filter becomes a Dirac pulse and the signal is not band-limited any more. What these examples illustrate is that testing with Dirac pulses and making blanket statements about ringing and their audibility shows a fundamental lack of understanding of sampling theory.

There is so much misinformation about what is the correct way to test a resampling algorithm, we perfectly understand if you do not trust us. Feel free to repeat these experiments with the band limited test file we used: Band-limited 44.1kHz impulse train and check for yourself using your preferred upsamplers.